Introduction to the Basic CHomP Software

The CHomP homology software is available in two configurations: a basic version that consists of a single command-line driven program chomp, with only a few fundamental features, and the full (advanced) version that is a package of several programs and a C++ programming library, with a variety of capabilities. This document is a tutorial on the features and usage of the basic version. To download the software or for documentation of the advanced version, use the links in the above menu. Please note that the CHomP website is under continuous development, with more material being added on a regular basis.

A primary application of the basic version of CHomP is the quantification of topological properties of an image or pattern. Some examples of projects which use this basic functionality are Evolution of Pattern Complexity during Phase Separation, Topological Characterization of Spiral Defect Chaos, and Topological Characterization of Spatial-Temporal Chaos. Here we will demonstrate how to use the basic program chomp to perform similar computations.

What does chomp compute?

The chomp program computes topological invariants called the Betti numbers of a collection of n-dimensional cubes. Betti numbers are part of the information contained in the homology groups of a topological space which intuitively measure the number of connected components, the number of holes, and the number of enclosed cavities in low dimensions. To illustrate these computations, consider the following set of 40,949 cubes contained in a cubical grid of size 247x287, which comes from numerical data generated from the Gray-Scott model, for more information see Topological Characterization of Spatial-Temporal Chaos.

The pixels colored in black in this picture are included in the space for which we want to analyze the topology and the white pixels are not. In other words, one should think of this as a black and white image and we want to measure the topology of the black region.

Suppose this picture is saved to a black-and-white Windows bitmap file bw_image.bmp (9 kB), or the integer coordinates of the black pixels are stored in a text file named bw_image.txt (300 kB) (we discuss the exact format below), then the command to compute the Betti numbers of this image would be:

chomp bw_image.txt     or     chomp bw_image.bmp

and the output would be:

3 20

Since this image is 2-dimensional, it can have at most two nonzero Betti numbers, in this case b0=3 and b1=20, and these numbers are displayed.

To illustrate what these two Betti numbers measure, we have colored the cubes in shades of red according to which connected component of the space the cube belongs. There are 3 connected components which is measured by b0=3.

Next we have outlined in black the holes which are completely enclosed by cubes / pixels in the colored region. One can easily count that there are 20 such white regions. The number of these holes is measured by b1=20.

An important point needs to be made here about the topology of an image / cubical set. In computations using chomp, pixels / cubes that intersect along lower dimensional faces such as vertices, or edges in three dimensions, are considered to be "connected." In the imaging literature, this is often referred to as considering (3d-1)-neighborhoods rather than (2d)-neighborhoods where d is the dimension of the image, see the example input below.

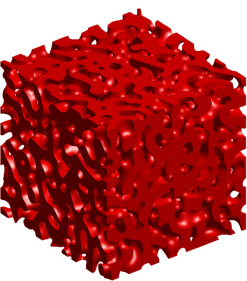Similar computations can be done with 3-dimensional images / cubical sets. The picture on the left was generated from the 3-dimensional Cahn-Hilliard equation, for more information see Evolution of Pattern Complexity during Phase Separation.

Since this image is 3-dimensional, it has three Betti numbers: b0=1, b1=1059, and b2=0. The Betti number b2 measures the number of completely enclosed cavities, such as the interior of a sphere. Thus, this computation indicates that the entire set of red cubes is connected since b0=1 and that there are no enclosed cavities since b2=0. The significance of b1=1059 is that this set has a large number of tunnels, like the interior of a cylinder, that wind through the space.

What is the input to chomp?

The chomp program accepts input files in a variety of different formats. In addition to Windows bmp files (binary images), it accepts multi-dimensional bitmaps (bmd files), and a few text file formats. Type chomp --files to have the list of all supported file formats with brief descriptions pritned to the screen (you may add |more to see this list page-by-page). The most intuitive one to use is a simplified "list of cubes" format, where each line is a space-delimited list of integer coordinates representing a cube or pixel. An input file for the black cubes in the picture to the left would be five lines:

  2  1
  2  2
  0  1
  1  0
  1  2

A simple Matlab function which takes as input a text file in this format and plots it as a black and white image is available here: plot_2dcubes.m.

The Betti numbers for this complex would be b0=1 and b1=1. Note that even though cubes (0,1) and (1,0) intersect only at a corner, they are considered to be connected and the entire complex has only one connected component so b0=1. Moreover, the cube (1,1) is a completely enclosed hole giving b1=1.

We emphasize again that the input is a binary (black and white) image. To compute the topology of patterns in a colored image the image / data must be thresholded to extract the set of pixels / cubes which represent the feature(s) of interest. Since this thresholding process is highly application dependent, the basic chomp program does not contain routines to threshold images / data. Issues concerning thresholding and noise can be significant. For some ideas about how users of chomp have dealt with some of these issues, consult the information at the various projects that use CHomP.

How to use the chomp program?

The program chomp is a command-line utility. This means that one has to open a terminal (or command prompt), enter the directory in which the executable program chomp is located (or add the program to the PATH), and type chomp (or ./chomp) followed by the name of a file in which the set of cubes for homology computation is stored, followed with optional arguments.

If the program chomp is run without any additional arguments, not even a file name, it shows brief information on its usage. Type chomp --help for more information. If the program is given a command-line argument which does not begin with the dash, the program opens a file with the given name, reads a cubical set from this file, computes its homology, and outputs the computed Betti numbers. No other information is output to the standard output stream, so one can embed a call to the program in a Perl script as $Betti = `chomp filename.txt` to get a string with space-separated Betti numbers.

Some command line arguments one may want to use are as follows:

How to download chomp?

Compiled versions of the program chomp are available for a few most popular operating systems at the download page. If you have trouble with these executables or need to compile for a different platform, you can download the source code and compile it using the GNU C++ compiler, see the compilation instructions below.

How to compile chomp?

After having downloaded the file chomp-src.zip, begin with creating an empty directory and unpacking this file into that directory. It is recommended to use the multi-platform Info-ZIP software for that purpose, and unpack the zip archive in the text mode:

unzip -a chomp-src.zip

The GNU make program, as well as the GNU C++ compiler is necessary to compile the chomp program; in Windows additionally PERL is required; for free distributions of C++ and Perl for MS-Windows, see e.g. wxDevCPP and ActivePerl, respectively.

Depending on the platform used, the compilation command is:

The executable program chomp is created in the bin subdirectory.

How to use the chomp library?

The basic source code for the chomp program contains a selection of files extracted from the CAPD and CHomP software libraries. In this distribution, a C++ function is defined for the homology computation of a set of cubes stored in the memory as an n-dimensional bitmap, which can be used from within one's own C++ programs. Please, refer to the files contained in the subdirectory examples/chompdemo for an example program that uses this library. The program is well commented, and the attached makefile should allow one to prepare a program which uses the library without hassle. In case of any doubt or if any additional information is necessary, don't hesitate to contact the CHomP group through the forum.

Are there any additional tools for chomp?

The developers and users of the CHomP software sometimes create certain helper programs, scripts, and tricks which can be useful to others, and a collection of some of these can be found on the chomp Tips page and / or the ChomP forum. Moreover, the "full version" of the source code of the CHomP library contains several programs for converting between various file formats or processing cubical sets. Please, refer to the descriptions displayed by each of the programs when run without arguments, or ask the progrms' authors for more details.

What are the algorithms used by chomp?

The program chomp incorporates sevaral engines for the homology computation. Each engine is an implementation of one algorithm. A brief description of these algorithms is displayed if one types chomp --engines, and the best engine is automatically chosen, depending on the input data. If one wants to use a specific engine for the computations, one should use the command-line argument --engine NAME (or -e NAME), where the name of the engine is one of the names displayed in the list, e.g. MM_CR.

Most algorithms used in the chomp program are based on local elementary reductions and collapses rather than performing standard matrix operations to compute homology. For a complete description which applies to some of the algorithms, see Computational Homology by Tomasz Kaczynski, Konstantin Mischaikow and Marian Mrozek (Appl. Math. Sci. Vol. 157, Springer Verlag, NY 2004).  Some other references include: [under construction]

How efficient is chomp?

[under construction]

This page was originally written by Bill Kalies, modified and expanded by Paweł Pilarczyk.